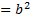Kamis, 28 Mei 2015
Rabu, 27 Mei 2015
Teorema Pythagoras
Dalil Pythagoras merupakan salah satu dalil yang sering digunakan secara luas. dalil ini pertama kali ditemukan oleh Phytagoras, yaitu seorang ahli matematika bangsa Yunani yang hidup dalam abad keenam masehi (kira-kira pada tahun 525 sebelum Masehi.
Salah satu peninggalan Phytagoras yang terkenal adalah teorema Phytagoras, yang menyatakan bahwa kuadrat hipotenusa adalah jumlah kuadrat dari kaki-kakinya. Walaupun fakta di dalam teorema ini telah banyak diketahui sebelum lahirnya Phytagoras, namun teorema ini dikreditkan kepada Phytagoras karena ia lah yang pertama membuktikan pengamatan ini secara matematis.
Sebelum mempelajari materi Pythagoras, kita membuktikan dahulu teorema yang dikemukakan oleh Phytagoras. Berikut adalah salah satu cara membuktikan teorema Phytagoras :
Keterangan gambar di atas:
1. Menghitung panjang salah satu sisi segitiga siku-siku jika kedua sisi lain diketahui.
Dengan menggunakan teorema Pythagoras kita dapat menghitung panjang salah satu sisi segitiga siku-siku jika panjang kedua sisi lain diketahui.


2. Untuk menentukan jenis segitiga
Pada materi di atas kita telah membahas mengenai pembuktian teorema Pythagoras. Untuk menentukan jenis segitiga kita menggunakan kebalikan teorema Pythagoras, yang berbunyi:
"untuk setiap segitiga jika jumlah kuadrat panjang dua sisi yang saling tegak lurus sama dengan kuadrat panjang sisi miring maka segitiga tersebut merupakan segitiga siku-siku".
Pada suatu segitiga berlaku:
3. Penggunaan teorema Pythagoras pada bangun datar dan bangun ruang
Selain dimanfaatkan pada segitiga siku-siku, teorema Pythagoras juga dapat digunakan pada bangun datar dan bagun ruang matematika yang lain untuk mencari panjang sisi-sisi yang belum diketahui.
Diagonal sisi adalah ruas garis yang menghubungkan dua titik sudut yang berhadapan pada suatu bidang datar.
Diagonal ruang adalah adalah ruas garis yang menghubungkan dua titik sudut yang berhadapan dalam suatu bangun ruang.


 merupakan diagonal sisi persegi panjang ABCD, dan
merupakan diagonal sisi persegi panjang ABCD, dan
 merupakan diagonal ruang balok ABCD.EFGH.
merupakan diagonal ruang balok ABCD.EFGH.
Sebagi contoh pada persegi panjang diatas diketahui panjang = 8, dan lebar = 6. Tentukan diagonal sisi persegi panjang tersebut.
Jawab:
untuk menjawabnya pertama yang kita amati segitiga ABC, karena sifat persegi panjang yang titik sudutnya merupakan siku-siku, maka segitiga ABC adalah segitiga siku-siku di B.
 maka kita dapat mencari panjang AC dengan menggunakan teorema Pythagoras.
maka kita dapat mencari panjang AC dengan menggunakan teorema Pythagoras.





Jadi, panjang AC adalah 10.
Contoh kedua kita dapat menggunakan balok ABCD.EFGH dengan panjang balok = 16 cm, lebar = 12 cm, dan tinggi balok 15 cm.
jawab:
Untuk menjawabnya pertama kita membuat garis bantu, berupa diagonal sisi ABCD. sehingga gambarnya menjadi
 kita dapat mencari panjang AC dengan cara seperti di atas
kita dapat mencari panjang AC dengan cara seperti di atas

 jadi panjang AC adalah 20cm. Setelah diketahui panjang AC maka kita
jadi panjang AC adalah 20cm. Setelah diketahui panjang AC maka kita
 dapat mencari panjang AG
dapat mencari panjang AG



 karena segitiga ACG merupakan segitiga siku-siku di C maka kita dapat menggunakan teorema Pythagoras.
karena segitiga ACG merupakan segitiga siku-siku di C maka kita dapat menggunakan teorema Pythagoras.

Dalil Pythagoras merupakan salah satu dalil yang sering digunakan secara luas. dalil ini pertama kali ditemukan oleh Phytagoras, yaitu seorang ahli matematika bangsa Yunani yang hidup dalam abad keenam masehi (kira-kira pada tahun 525 sebelum Masehi.
Salah satu peninggalan Phytagoras yang terkenal adalah teorema Phytagoras, yang menyatakan bahwa kuadrat hipotenusa adalah jumlah kuadrat dari kaki-kakinya. Walaupun fakta di dalam teorema ini telah banyak diketahui sebelum lahirnya Phytagoras, namun teorema ini dikreditkan kepada Phytagoras karena ia lah yang pertama membuktikan pengamatan ini secara matematis.
Sebelum mempelajari materi Pythagoras, kita membuktikan dahulu teorema yang dikemukakan oleh Phytagoras. Berikut adalah salah satu cara membuktikan teorema Phytagoras :
 |
| Pembuktian Teorema Pythagoras |
Misalkan panjang sisi miring (hipotenusa) dari segitiga siku-siku diatas adalah c, dan pajang 2 sisi yang lain berturut-turut adalah a, dan b.
Maka :
Dari gambar diatas dapat dilihat bahwa luas persegi hijau sama dengan luas persegi merah di tambah luas persegi orange, atau secara matematika dituliskan sebagai berikut 

Dengan cara seperti itu maka terbukti kuadrat panjang sisi miring (hipotenusa) sebuah segitiga siku-siku adalah jumlah kuadrat panjang sisi-sisi yang lain.
maka dapat diperoleh juga rumus-rumus sebagai berikut :
dengan c adalah panjang sisi miring segitiga siku-siku, serta a, dan b adalah panjang sisi-sisi segitiga yang saling tegak lurus.
Penggunaan Teorema Pythagoras
Kegunaan dari teorema Pythagoras ini adalah sebagai berikut :
- Menghitung panjang salah satu sisi segitiga siku-siku jika kedua sisi lain diketahui.
- Untuk menentukan jenis suatu segitiga.
- Digunakan pada bangun datar dan bangun ruang.
1. Menghitung panjang salah satu sisi segitiga siku-siku jika kedua sisi lain diketahui.
Dengan menggunakan teorema Pythagoras kita dapat menghitung panjang salah satu sisi segitiga siku-siku jika panjang kedua sisi lain diketahui.
sebagai contoh, tentukan panjang sisi yang belum diketahui! Jawab
Jawab
 Jawab
Jawab

2. Untuk menentukan jenis segitiga
Pada materi di atas kita telah membahas mengenai pembuktian teorema Pythagoras. Untuk menentukan jenis segitiga kita menggunakan kebalikan teorema Pythagoras, yang berbunyi:
"untuk setiap segitiga jika jumlah kuadrat panjang dua sisi yang saling tegak lurus sama dengan kuadrat panjang sisi miring maka segitiga tersebut merupakan segitiga siku-siku".
Pada suatu segitiga berlaku:
- Jika kuadrat sisi miring = julah kuadrat sisi yang lain maka segitiga tersebut siku-siku.
- Jika kuadrat sisi miring < jumlah kuadrat sisi yang lain maka segitiga tersebut lancip.
- Jika kuadrat sisi miring > jumlah kuadrat sisi yang lain maka segitiga tersebut tumpul.
3. Penggunaan teorema Pythagoras pada bangun datar dan bangun ruang
Selain dimanfaatkan pada segitiga siku-siku, teorema Pythagoras juga dapat digunakan pada bangun datar dan bagun ruang matematika yang lain untuk mencari panjang sisi-sisi yang belum diketahui.
Diagonal sisi adalah ruas garis yang menghubungkan dua titik sudut yang berhadapan pada suatu bidang datar.
Diagonal ruang adalah adalah ruas garis yang menghubungkan dua titik sudut yang berhadapan dalam suatu bangun ruang.


 merupakan diagonal sisi persegi panjang ABCD, dan
merupakan diagonal sisi persegi panjang ABCD, dan
 merupakan diagonal ruang balok ABCD.EFGH.
merupakan diagonal ruang balok ABCD.EFGH.Sebagi contoh pada persegi panjang diatas diketahui panjang = 8, dan lebar = 6. Tentukan diagonal sisi persegi panjang tersebut.
Jawab:
untuk menjawabnya pertama yang kita amati segitiga ABC, karena sifat persegi panjang yang titik sudutnya merupakan siku-siku, maka segitiga ABC adalah segitiga siku-siku di B.
 maka kita dapat mencari panjang AC dengan menggunakan teorema Pythagoras.
maka kita dapat mencari panjang AC dengan menggunakan teorema Pythagoras.




Jadi, panjang AC adalah 10.
Contoh kedua kita dapat menggunakan balok ABCD.EFGH dengan panjang balok = 16 cm, lebar = 12 cm, dan tinggi balok 15 cm.
jawab:
Untuk menjawabnya pertama kita membuat garis bantu, berupa diagonal sisi ABCD. sehingga gambarnya menjadi
 kita dapat mencari panjang AC dengan cara seperti di atas
kita dapat mencari panjang AC dengan cara seperti di atas
 jadi panjang AC adalah 20cm. Setelah diketahui panjang AC maka kita
jadi panjang AC adalah 20cm. Setelah diketahui panjang AC maka kita  dapat mencari panjang AG
dapat mencari panjang AG


 karena segitiga ACG merupakan segitiga siku-siku di C maka kita dapat menggunakan teorema Pythagoras.
karena segitiga ACG merupakan segitiga siku-siku di C maka kita dapat menggunakan teorema Pythagoras. 
Sehingga panjang diagonal ruang balok adalah 25 cm.
Semoga apa yang kami sampaikan disini cukup untuk membantu dalam mempelajari teorema Pythagoras. Bila ada kesalahan di dalam menjelaskan, maka kami mohon maaf atas kesalahan kami. Terimakasih.
Laurensius Andi Saputra
David Hantoro
Fausi Setiawan
Langganan:
Komentar (Atom)